In the last chapter we iterated over a simple graph using Bellman-Ford to find the shortest paths from a single vertex (our source) to all other vertices in the graph.

The complexity of Bellman-Ford is O(|V| E), which can approximate O(n^2) if every vertex has at least one outgoing edge. In other words: it's not terribly efficient.

Dijkstra's algorithm requires only one iteration, however and has a complexity of O(|V| log V), which is much more efficient.

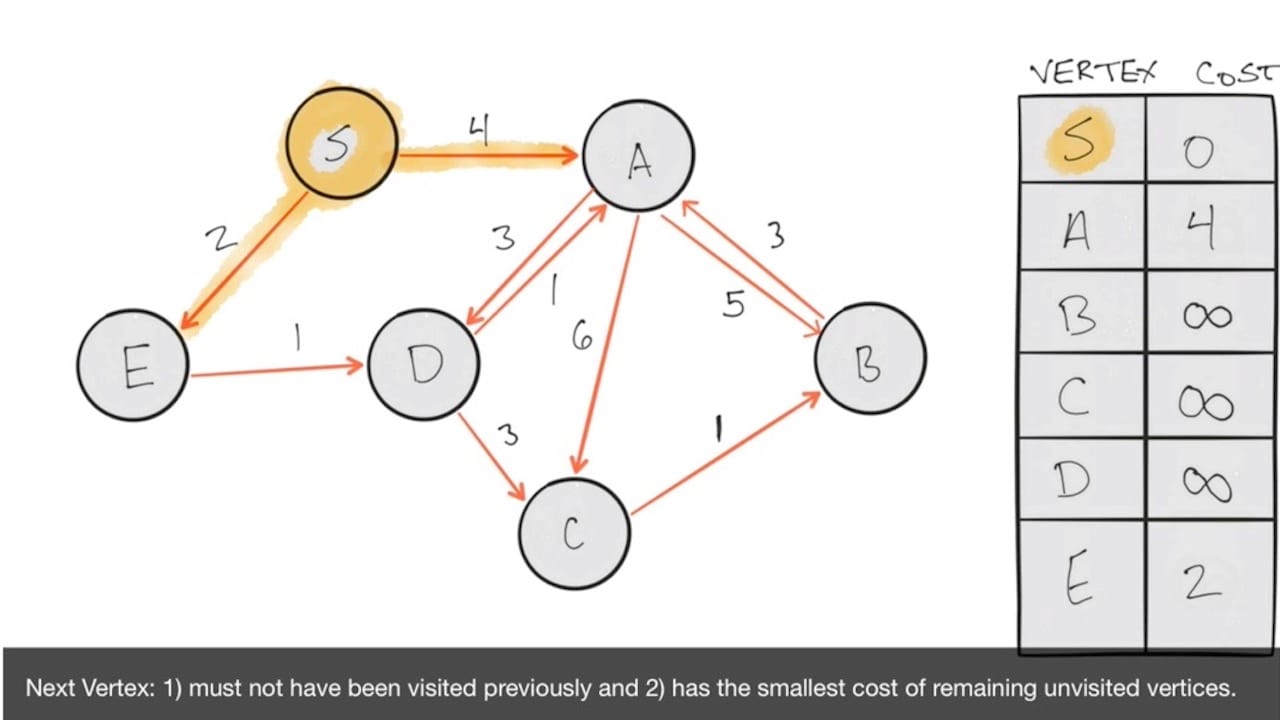
As with Bellman-Ford, we'll use a directed, weighted graph with 6 vertices. In addition, we'll setup a memo table with our source S set to 0 and the rest of the vertices set to infinity.

There is a difference here, however, and it's critical! Dijkstra doesn't work with negative edge weights! I have adjusted this graph so that we don't have any negative weights, as you can see. Specifically the edges between S and E as well as C to B. In addition I've added a few edges to show that the algorithm will scale easily regardless of the number of edges involved.

//Dijkstra: Shortest path calculation
//on an edge-weighted, directed graph
class MemoTable{
  constructor(vertices){
    this.S = {name: "S", cost: 0, visited: false};
    this.table = [this.S];
    for(var vertex of vertices){
      this.table.push({name: vertex, cost: Number.POSITIVE_INFINITY, visited: false});
    }
  };
  getCandidateVertices(){
   return this.table.filter(entry => {
     return entry.visited === false;
   });
  };
  nextVertex(){
   const candidates = this.getCandidateVertices();
   if(candidates.length > 0){
     return candidates.reduce((prev, curr) => {
       return prev.cost < curr.cost ? prev : curr;
     });
   }else{
     return null;
   }
  };
  setCurrentCost(vertex, cost){
    this.getEntry(vertex).cost =cost;
  };
  setAsVisited(vertex){
    this.getEntry(vertex).visited = true;
  };
  getEntry(vertex){
    return this.table.find(entry => entry.name == vertex);
  };
  getCost(vertex){
    return this.getEntry(vertex).cost;
  };
  toString(){
    console.log(this.table);
  }
};
const vertices = ["A", "B","C", "D", "E"];
const graph = [
  {from : "S", to :"A", cost: 4},
  {from : "S", to :"E", cost: 2},
  {from : "A", to :"D", cost: 3},
  {from : "A", to :"C", cost: 6},
  {from : "A", to :"B", cost: 5},
  {from : "B", to :"A", cost: 3},
  {from : "C", to :"B", cost: 1},
  {from : "D", to :"C", cost: 3},
  {from : "D", to :"A", cost: 1},
  {from : "E", to: "D", cost: 1}
]
const memo = new MemoTable(vertices);
const evaluate = vertex => {
  const edges = graph.filter(path => {
    return path.from === vertex.name;
  });
  for(edge of edges){
    const currentVertexCost = memo.getCost(edge.from);
    const toVertexCost = memo.getCost(edge.to);
    const tentativeCost = currentVertexCost + edge.cost;
    if(tentativeCost < toVertexCost){
      memo.setCurrentCost(edge.to, tentativeCost);
    }
  };
  memo.setAsVisited(vertex.name);
  const next = memo.nextVertex();
  if(next) evaluate(next);
}
//kick it off from the source vertex
evaluate(memo.S);
memo.toString();