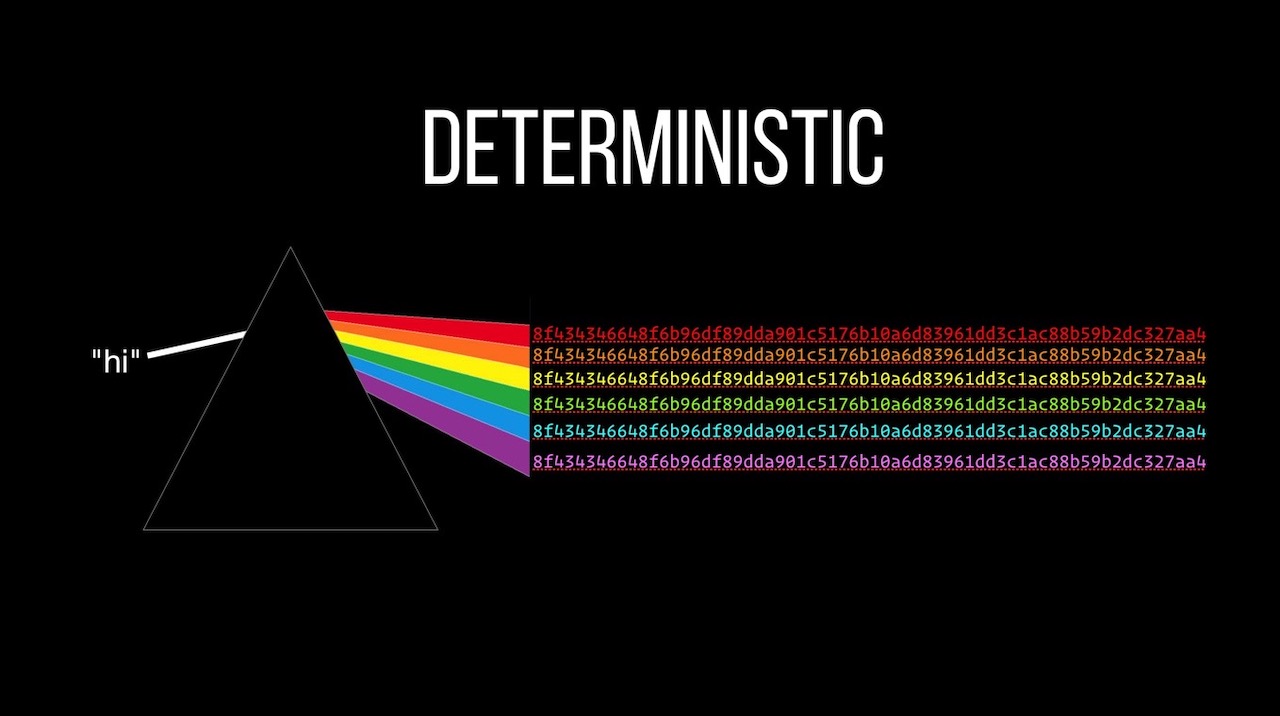
In this video we dive into hashing algorithms, how they're used and what they're good (and not so good) for. We'll also dig into RSA, one of the most important pieces of software ever created.
I've used hashes for a long time and had a general understanding of what they do... but that's about it. I knew I needed to hash passwords (and other secure data) if I was going to store them in my database... but that's about all.
I was never sure which algorithms to use nor why... so I dug in and found out. That's the first part of this video.
The second is asymmetric encryption: encoding with a public key and decoding with a second, private key. Absolutely ground-breaking idea! The math is amazingly straightforward too... although I will admit to struggling to explain some of it.
The Code
To produce a simple hash using Node:
const crypto = require("crypto");
const hash = crypto.createHash("sha256")
.update("hi")
.digest("hex");
console.log(hash);
Hashing a password with PBKDF2 using a million rounds to slow things down:
const crypto = require("crypto");
const hashPassword = function(pw){
return new Promise(function(resolve, reject){
crypto.pbkdf2(pw,"super-secret-salt",1000000,32,"sha512", function(err, buffer){
if(err) reject(err);
else resolve(buffer.toString("hex"))
});
})
}
Hashing using scrypt, assigning a cost:
const hashPassword = function(pw){
return new Promise(function(resolve, reject){
crypto.scrypt(pw,"super-secret-salt",32, {cost: 2**14}, function(err, buffer){
if(err) reject(err);
else resolve(buffer.toString("hex"))
});
})
}
Creating a checksum using MD5:
const crypto = require("crypto");
const fs = require("fs");
const data = fs.readFileSync("./message.txt");
const checksum = function(data){
return crypto.createHash("md5").update(data, "utf8").digest("hex")
}
console.log(checksum(data));
A super-simple mining operation (meant for demonstration only) for blockchain stuff:
const crypto = require("crypto");
const createHash = (block) => {
//need to pass a string to our
const hashValue = JSON.stringify(block)
return crypto.createHash("sha256")
.update(hashValue)
.digest("base64");
}
const mine = (block, difficulty = 2) => {
let found = false, start = new Date().getTime();
//we're looking for a string of 0s so let's create the pattern
//I could use Regex but I'm not that good
const lookingFor = "0".padStart(difficulty, "0");
console.log("Looking for a hash starting with", lookingFor);
const duration = new Date().getTime() - start;
while(!found){
const possibleHash = createHash(block);
//does the hash start with zeroes?
found = possibleHash.substring(0, difficulty) === lookingFor;
if(found){
block.hashKey = possibleHash;
return block;
}
block.nonce += 1;
//10 second kill switch
if(duration > 10000) return "Didn't find it under 10s"
}
}
const block = {
transactions: [
{from: "me", to: "you", amount: 10.00},
{from: "you", to: "me", amount: 5.00}
],
timestamp: 1609702546153, //if this changes the hash changes
nonce: 0,
previousKey: "00RSDThMVcQAvoocD3klO/6pjJ4a8pRbZ3ykk3XXhXE="
}
//let's see how long this takes
const start = new Date().getTime();
//let's do it!
const result = mine(block, 4);
const duration = new Date().getTime() - start;
console.log(`That took duration ${duration}ms`);
console.log(result);
And finally, our trip through the basics of RSA using super small primes:
//resources
//https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html
//https://www.cryptool.org/en/cto/highlights/rsa-step-by-step
//let's find two relatively prime numbers, e and d, such that
//e % d mod r === 1
//this is the cornerstone of RSA
var findEandD = function(r) {
//These are common candidates for e, which can be autoset
//and typically 65537 is used, but we'll
//start small for speed
const possibleEs = [3n,5n,17n,257n,65537n]
//now, loop over the possible e's so we can find our d
for(let e of possibleEs){
//we want to find a coprime for e, so let's factor it
//up to r and see if e % r is 1
//if it is, we found our coprime
for (let d = 1n; d < r; d++) {
const candidate = e * d;
if (candidate % r == 1n) return {e: e, d: d};
}
}
assert.fail("We shouldn't reach this point")
}
const p = 499n;
const q = 491n;
assert.notStrictEqual(p,q, "p and q must be different primes");
//our public key, N
const N = p * q;
//Euler's totient for deriving r
//r = phi(n) = (p-1) * (q-1)
const r = (p-1n) * (q-1n);
//now we can calculate e and d for our private key
const {e,d} = findEandD(r);
//our message
const M = 25n;
console.log("e",e);
console.log("d",d);
console.log("N",N);
console.log("r",r);
console.log("M", M);
//the RSA algorithm
const encrypted = M**e % N;
const decrypted = encrypted**d % N;
console.log("Encrypted",encrypted);
console.log("Decrypted",decrypted);
Links and Resources
I cite a number of articles in this video - hard not to. But here they are if you want to read more: