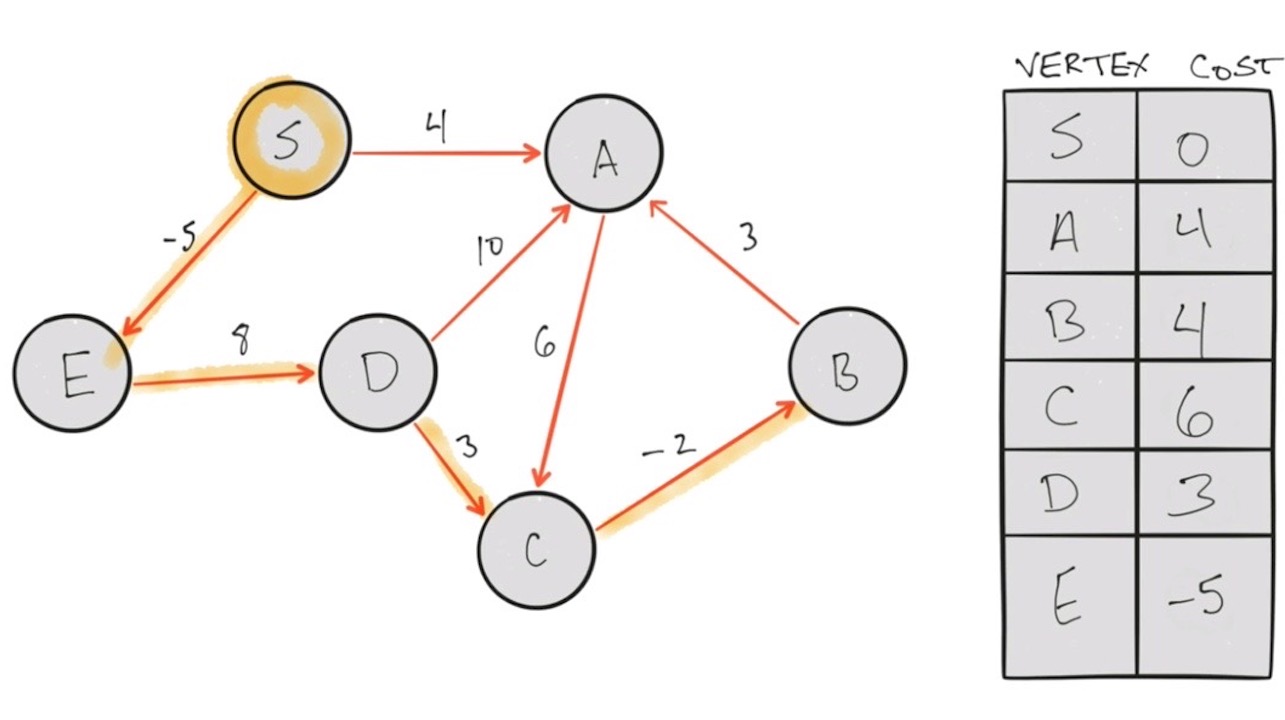
How can you traverse a graph ensuring you take the route with the lowest cost? The Bellman-Ford algorithm will answer this question.
One of the most fascinating uses of graphs is in the optimization of path traversal, which can be used in a vast number of calculations.
As mentioned in the previous chapter, graphs can be used to represent all kinds of information:
- A network of any kind. Social (friends) or digital (computers or the internet), for example
- A decision tree
- Contributions from members of any kind to a cause of any kind
- Atomic interactions in physics, chemistry or biology
Navigation between various endpoints - If you apply weighting to the edges or vertices, you can run useful calculations for just about anything. One of the most common is finding the shortest path between two vertices.
//Bellman-Ford: Shortest path calculation
//on an edge-weighted, directed graph
const vertices = ["S", "A", "B", "C", "D", "E"];
var memo = {
S:0,
A:Number.POSITIVE_INFINITY,
B:Number.POSITIVE_INFINITY,
C:Number.POSITIVE_INFINITY,
D:Number.POSITIVE_INFINITY,
E:Number.POSITIVE_INFINITY
};
const graph = [
{from : "S", to : "A", cost: 4},
{from : "S", to :"E", cost: -5},
{from : "A", to :"C", cost: 6},
{from : "B", to :"A", cost: 3},
{from : "C", to :"B", cost: -2},
{from : "D", to :"C", cost: 3},
{from : "D", to :"A", cost: 10},
{from : "E", to: "D", cost: 8}
];
const iterate = () => {
var doItAgain = false;
for(fromVertex of vertices){
const edges = graph.filter(path => {
return path.from === fromVertex;
});
for(edge of edges){
const potentialCost = memo[edge.from] + edge.cost;
if(potentialCost < memo[edge.to]){
memo[edge.to] = potentialCost;
doItAgain = true;
}
}
}
return doItAgain;
}
for(vertex of vertices){
if(!iterate()) break;
}
console.log(memo);